The Figge-Fencl Quantitative Physicochemical Model
of Human Acid-Base Physiology (Version 3.0)
by James J. Figge, MD, MBA
Copyright 2003 - 2026 James J. Figge.
Published 8 October, 2012; updated on 28 April, 2013;
updated on 27 October, 2013;
on www.acid-base.org.
Statistical Validation of the Figge-Fencl Quantitative
Physicochemical Model
(Version 3.0)
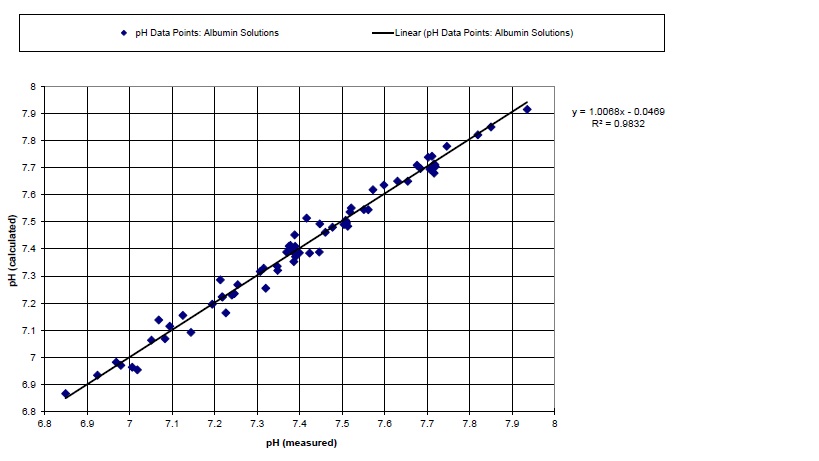
Figure 1. pH of albumin-containing solutions as calculated by the
Figge-Fencl quantitative physicochemical model (version 3.0) (y-axis), versus
measured pH (x-axis). Experimental data cover the pH range of 6.85 to 7.94. Experimental
data (n = 65) are from Figge, Rossing and Fencl, J Lab Clin Med. 1991; 117: 453-467.
The slope of the regression line is 1.0068 (98% confidence limits: 0.9672 to 1.0464). Thus,
the slope is not significantly different than 1.0000. The intercept is -0.0469.
R = 0.99157, and R2 = 0.9832.
Paired t Test.
The mean difference, { Σ(calculated pH - measured pH) } / 65 = 0.0034 (+/- 0.0329 Standard Deviation).
The 98% confidence interval for the mean difference is calculated using: t (n-1, alpha/2) = 2.386; where n = 65; alpha=0.02.
The 98% confidence interval for the mean difference is 0.0034 +/- (2.386)(0.0329)/SQRT(65) = 0.0034 +/- 0.0097.
Hence, the mean difference is not statistically different than zero.
Reference Data
Sample Number, SID, PCO2, Pi, Albumin, Measured pH, Calculated pH, Difference, Difference Squared
DATA 1 , 49.8 , 39.3 , 1.1 , 7.2 , 7.388 , 7.45186896168161 , 6.38689616816119E-02 , 4.07924426628721E-03
DATA 2 , 45.4 , 40 , 1 , 7 , 7.383 , 7.39164865761995 , 8.64865761995315E-03 , 7.47992786271737E-05
DATA 3 , 45.4 , 26.1 , 1 , 7 , 7.521 , 7.55122460937127 , 3.02246093712748E-02 , 9.13527011646153E-04
DATA 4 , 45.4 , 38.1 , 1 , 7 , 7.389 , 7.40980515582487 , 2.08051558248696E-02 , 4.32854508897107E-04
DATA 5 , 45.4 , 62.9 , 1 , 7 , 7.217 , 7.22307206084952 , 6.07206084951795E-03 , 3.68699229602486E-05
DATA 6 , 32.2 , 23.4 , 1.2 , 6.6 , 7.315 , 7.32882901327685 , 1.38290132768448E-02 , 1.9124160821115E-04
DATA 7 , 32.2 , 35 , 1.2 , 6.6 , 7.194 , 7.19565304508433 , 1.65304508432751E-03 , 2.73255805081934E-06
DATA 8 , 32.2 , 68.6 , 1.2 , 6.6 , 6.979 , 6.97039783885702 ,-8.60216114297518E-03 , 7.39971763297121E-05
DATA 9 , 71.3 , 28.9 , 1.1 , 6.8 , 7.819 , 7.82143116742373 , 2.43116742372518E-03 , 5.91057504218252E-06
DATA 10 , 71.3 , 37.7 , 1.1 , 6.8 , 7.716 , 7.71349582821131 ,-2.50417178869267E-03 , 6.27087634728423E-06
DATA 11 , 71.3 , 65.4 , 1.1 , 6.8 , 7.504 , 7.49055102257989 ,-1.34489774201061E-02 , 1.80874993646523E-04
DATA 12 , 70.2 , 26.4 , 1 , 6.8 , 7.85 , 7.8502791498322 , 2.7914983220434E-04 , 7.79246288197109E-08
DATA 13 , 70.2 , 37.9 , 1 , 6.8 , 7.719 , 7.70358445285819 ,-1.54155471418056E-02 , 2.37639093681231E-04
DATA 14 , 70.2 , 65.3 , 1 , 6.8 , 7.513 , 7.48366857494693 ,-2.93314250530674E-02 , 8.6033249564371E-04
DATA 15 , 45.9 , 30.8 , 1 , 7.1 , 7.447 , 7.49262359552085 , 4.56235955208539E-02 , 2.08151246825048E-03
DATA 16 , 45.9 , 38.4 , 1 , 7.1 , 7.375 , 7.41029045451432 , 3.52904545143247E-02 , 1.24541617982762E-03
DATA 17 , 45.9 , 85 , 1 , 7.1 , 7.094 , 7.11468532006256 , 2.06853200625625E-02 , 4.27882466090651E-04
DATA 18 , 70.2 , 22.5 , 1 , 6.8 , 7.935 , 7.91523252509069 ,-1.97674749093126E-02 , 3.90753064290304E-04
DATA 19 , 70.2 , 40.2 , 1 , 6.8 , 7.716 , 7.6797193539096 ,-3.62806460903959E-02 , 1.31628528073656E-03
DATA 20 , 70.2 , 83.5 , 1 , 6.8 , 7.423 , 7.38464369426947 ,-3.83563057305292E-02 , 1.47120618929383E-03
DATA 21 , 45.8 , 22.1 , 1 , 3.5 , 7.746 , 7.77916299365461 , 3.31629936546083E-02 , 1.09978414813559E-03
DATA 22 , 45.8 , 39.9 , 1 , 3.5 , 7.518 , 7.53625158267096 , 1.82515826709571E-02 , 3.3312026999478E-04
DATA 23 , 45.8 , 85.9 , 1 , 3.5 , 7.218 , 7.22261464502662 , 4.61464502662423E-03 , 2.12949487217478E-05
DATA 24 , 24.2 , 21.9 , 0.9 , 3.4 , 7.446 , 7.3886169437319 ,-5.73830562680957E-02 , 3.29281514666744E-03
DATA 25 , 24.2 , 39.8 , 0.9 , 3.4 , 7.226 , 7.16390463616699 ,-6.20953638330102E-02 , 3.85583420955391E-03
DATA 26 , 24.2 , 69.7 , 0.9 , 3.4 , 7.018 , 6.95350919384509 ,-6.44908061549065E-02 , 4.15906407850973E-03
DATA 27 , 63.7 , 40.2 , 1 , 3.6 , 7.676 , 7.70913776068483 , 3.31377606848253E-02 , 1.09811118320475E-03
DATA 28 , 63.7 , 86.7 , 1 , 3.6 , 7.369 , 7.38836321781855 , 0.019363217818551 , 3.74934204288651E-04
DATA 29 , 75.5 , 38.6 , 1 , 6.7 , 7.711 , 7.74218448600732 , 3.11844860073176E-02 , 9.72472167540587E-04
DATA 30 , 76.4 , 38.2 , 1 , 7.3 , 7.702 , 7.73856468789745 , 3.65646878974513E-02 , 1.33697640103802E-03
DATA 31 , 65.9 , 37.9 , 1 , 7.3 , 7.63 , 7.65034119295888 , 2.03411929588766E-02 , 4.13764130990251E-04
DATA 32 , 60.2 , 35.1 , 0.7 , 7.6 , 7.572 , 7.61867349362001 , 4.66734936200082E-02 , 2.17841500669694E-03
DATA 33 , 58.9 , 41 , 1 , 1.7 , 7.718 , 7.71041089866776 ,-7.58910133223978E-03 , 5.75944590310036E-05
DATA 34 , 58.9 , 67.9 , 1 , 1.7 , 7.51 , 7.49600895750336 ,-1.39910424966363E-02 , 1.95749270142683E-04
DATA 35 , 58.9 , 88 , 1 , 1.7 , 7.399 , 7.38586627563927 ,-1.31337243607268E-02 , 1.72494715583548E-04
DATA 36 , 70.4 , 38.2 , 1 , 7 , 7.684 , 7.69671562733129 , 1.27156273312865E-02 , 1.6168717842816E-04
DATA 37 , 70.4 , 65.4 , 1 , 7 , 7.477 , 7.47992098843679 , 2.92098843678801E-03 , 8.53217344784925E-06
DATA 38 , 70.4 , 85.7 , 1 , 7 , 7.39 , 7.37133328034543 ,-1.86667196545747E-02 , 3.48446422662484E-04
DATA 39 , 53.5 , 38.7 , 1 , 6.2 , 7.551 , 7.54521409911104 ,-5.78590088896469E-03 , 3.34766490969224E-05
DATA 40 , 53.5 , 68.4 , 1 , 6.2 , 7.348 , 7.32078778464347 ,-2.72122153565286E-02 , 7.40504664610092E-04
DATA 41 , 53.5 , 86.3 , 1 , 6.2 , 7.24 , 7.22954700456467 ,-0.010452995435335 , 1.09265113571133E-04
DATA 42 , 51.2 , 41.2 , 0.9 , 1.9 , 7.598 , 7.63584546966013 , 3.78454696601258E-02 , 1.4322795737955E-03
DATA 43 , 51.2 , 69.8 , 0.9 , 1.9 , 7.378 , 7.41301136161201 , 3.50113616120069E-02 , 1.22579544192671E-03
DATA 44 , 51.2 , 87.7 , 0.9 , 1.9 , 7.307 , 7.31663671531715 , 9.63671531714461E-03 , 9.28662821036895E-05
DATA 45 , 32.5 , 22.5 , 1 , 8 , 7.32 , 7.25471883593127 ,-0.065281164068729 , 4.26163038216831E-03
DATA 46 , 32.5 , 38.9 , 1 , 8 , 7.144 , 7.09191065700725 ,-5.20893429927529E-02 , 2.71329965341666E-03
DATA 47 , 32.5 , 59.2 , 1 , 8 , 7.006 , 6.96329846512526 ,-4.27015348747375E-02 , 1.82342108065842E-03
DATA 48 , 28.5 , 22.7 , 1 , 2.9 , 7.416 , 7.51374596869573 , 9.77459686957296E-02 , 9.55427439626655E-03
DATA 49 , 28.5 , 40.3 , 1 , 2.9 , 7.213 , 7.28575872583315 , 7.27587258331477E-02 , 5.29383218486315E-03
DATA 50 , 28.5 , 58.6 , 1 , 2.9 , 7.068 , 7.13776919478551 , 6.97691947855059E-02 , 4.86774054101787E-03
DATA 51 , 22.8 , 23.1 , 1 , 1.6 , 7.46 , 7.46129691042006 , 1.29691042006019E-03 , 1.68197663766071E-06
DATA 52 , 22.8 , 40.2 , 1 , 1.6 , 7.246 , 7.23515126854181 ,-1.08487314581875E-02 , 1.17694974251868E-04
DATA 53 , 22.8 , 60.6 , 1 , 1.6 , 7.083 , 7.06834687432274 ,-0.014653125677258 , 2.14714092113517E-04
DATA 54 , 23.7 , 22.6 , 1 , 5.7 , 7.125 , 7.15467195678502 , 2.96719567850232E-02 , 8.80425019452285E-04
DATA 55 , 23.7 , 40 , 1 , 5.7 , 6.968 , 6.981773449108 , 1.37734491080046E-02 , 1.89707900330793E-04
DATA 56 , 23.7 , 58 , 1 , 5.7 , 6.849 , 6.86582762748003 , 1.68276274800299E-02 , 2.83169046606656E-04
DATA 57 , 21.4 , 23 , 1 , 3.5 , 7.254 , 7.26822499139234 , 1.42249913923447E-02 , 2.0235038011228E-04
DATA 58 , 21.4 , 40.7 , 1 , 3.5 , 7.051 , 7.06323277764022 , 1.22327776402233E-02 , 1.49640848795148E-04
DATA 59 , 21.4 , 58.3 , 1 , 3.5 , 6.924 , 6.93370805447921 , 9.70805447921119E-03 , 9.42463217713325E-05
DATA 60 , 67.5 , 39.7 , 1 , 7.2 , 7.654 , 7.64973710908089 ,-4.26289091911158E-03 , 1.8172238988244E-05
DATA 61 , 67.5 , 56.9 , 1 , 7.2 , 7.508 , 7.50571109482553 ,-2.28890517447145E-03 , 5.23908689772216E-06
DATA 62 , 67.5 , 87 , 1 , 7.2 , 7.347 , 7.33646802732255 ,-1.05319726774473E-02 , 1.10922448478497E-04
DATA 63 , 62.5 , 40.1 , 1 , 3.8 , 7.706 , 7.69481228571385 ,-0.011187714286149 , 1.25164950948501E-04
DATA 64 , 62.5 , 57.5 , 1 , 3.8 , 7.561 , 7.54473308031447 ,-1.62669196855276E-02 , 2.64612676055406E-04
DATA 65 , 62.5 , 91.2 , 1 , 3.8 , 7.386 , 7.35308220679872 ,-3.29177932012827E-02 , 1.08358110924242E-03
N = 65
Checksum1 for pHm = 481.218
Checksum2 for SID = 3194.9
Checksum3 for PCO2 = 3210.8
Checksum4 for Pi = 65.1
Checksum5 for Alb = 342.8
Checksum6 for pH = 481.439307340304
Sum of Deviations = 0.221307340304365
Mean Deviation = 3.40472831237484E-03
Sum of Absolute Deviations = 1.63638280045148
Mean Absolute Deviation = 2.51751200069458E-02
Sum of Squares of Deviations = 7.00002270873043E-02
Root Mean Square Deviation = 3.28165593957367E-02
Standard Deviation = 3.28934681300942E-02
HIS14 = 5.1
HIS15 = 6.7
HIS16 = 6.2
LYS1 = 5.8 , n1 = 2
LYS2 = 6.15 , n2 = 2
LYS3 = 7.51 , n3 = 2
LYS4 = 7.685 , n4 = 2
LYS5 = 7.86 , n5 = 1
LYS6 = 10.3 , n6 = 50
slope = 1.00678874215608
intercept = -4.68547320397751E-02
intercept = -4.68547320394102E-02 (verify)
r = 0.991565222939416
r^2 = 0.983201591342893
Variance = 1.09623723925786E-03
Variance of slope = 2.74891760302995E-04
Stnd Deviation of slope = 1.65798600809233E-02
98% confidence interval for the slope = 0.967212616142919 to 1.04636486816925
Source Code
Note: This code is for educational use only; it is not to be used for clinical purposes.
Sub Model()
Rem: Figge-Fencl Quantitative Physicochemical Model
Rem: of Human Acid-Base Physiology (Version 3.0).
Rem:
Rem: Program by James J. Figge, MD, MBA. Updated September, 2012.
Rem: Copyright 2003 - 2022 James J. Figge. Published 8 October, 2012.
Close #1
Dim pHm(65), SID(65), PCO2(65), Pi(65), Alb(65)
rownum = 1
colnum = 1
rownum = ActiveCell.Row
colnum = ActiveCell.Column
Worksheets("Sheet1").Activate
sum1 = 0
sum2 = 0
sum3 = 0
sum4 = 0
sum5 = 0
For rownum = 1 To 65
pHm(rownum) = ActiveSheet.Cells(rownum, 2)
SID(rownum) = ActiveSheet.Cells(rownum, 3)
PCO2(rownum) = ActiveSheet.Cells(rownum, 4)
Pi(rownum) = ActiveSheet.Cells(rownum, 5)
Alb(rownum) = ActiveSheet.Cells(rownum, 6)
sum1 = sum1 + pHm(rownum)
sum2 = sum2 + SID(rownum)
sum3 = sum3 + PCO2(rownum)
sum4 = sum4 + Pi(rownum)
sum5 = sum5 + Alb(rownum)
Next rownum
Rem: Kc1 is derived from the parameters in the Henderson-Hasselbalch
Rem: equation. pK = 6.1; a = 0.230 mM / kPa; 1 Torr = 0.13332236842105 kPa
Rem: The value of Kc1 is 2.44E-11 (Eq / L)^2 / Torr.
Rem: Kc2 is calculated from Harned and Scholes (1941) for 37 degrees C and ionic
Rem: strength 0.15 M. The value of Kc2 is 5.5E-11 mol / L x 2 = 1.1E-10 Eq / L.
Rem: K1, K2, and K3 for the phosphoric acid - phosphate system are from Sendroy and
Rem: Hastings (1927).
Const kw = 0.000000000000044
Const Kc1 = 0.0000000000244
Const Kc2 = 0.00000000011
Const K1 = 0.0122
Const K2 = 0.000000219
Const K3 = 0.00000000000166
Const LYS1 = 5.8
Const LYS2 = 6.15
Const LYS3 = 7.51
Const LYS4 = 7.685
Const LYS5 = 7.86
Const LYS6 = 10.3
Const HIS14 = 5.1
Const HIS15 = 6.7
Const HIS16 = 6.2
ss = 0
s = 0
abvs = 0
sx = 0
sxx = 0
sy = 0
syy = 0
sxy = 0
sum6 = 0
Open "albumin-pH-output" For Output As #2
For j = 1 To 65
High = 14
Low = 1
calculatepH:
pH = (High + Low) / 2
Rem: H is hydrogen ion activity (also used as an approximation of [H+])
H = 10 ^ -pH
HCO3 = Kc1 * PCO2(j) / H
CO3 = Kc2 * HCO3 / H
FNX = K1 * H * H + 2 * K1 * K2 * H + 3 * K1 * K2 * K3
FNY = H * H * H + K1 * H * H + K1 * K2 * H + K1 * K2 * K3
FNZ = FNX / FNY
P = Pi(j) * FNZ
Netcharge = SID(j) + 1000 * (H - kw / H - HCO3 - CO3) - P
Rem: NB accounts for histidine pK shift due to the NB transition
NB = 0.4 * (1 - (1 / (1 + (10 ^ (pH - 6.9)))))
Rem: Calculate charge on albumin
Rem: alb2 accumulates results
Rem: cysteine residue
alb2 = -1 / (1 + 10 ^ (-(pH - 8.5)))
Rem: glutamic acid and aspartic acid residues
alb2 = alb2 - 98 / (1 + 10 ^ (-(pH - 3.9)))
Rem: tyrosine residues
alb2 = alb2 - 18 / (1 + 10 ^ (-(pH - 11.7)))
Rem: arginine residues
alb2 = alb2 + 24 / (1 + 10 ^ (pH - 12.5))
Rem: lysine residues
alb2 = alb2 + 2 / (1 + 10 ^ (pH - LYS1))
alb2 = alb2 + 2 / (1 + 10 ^ (pH - LYS2))
alb2 = alb2 + 2 / (1 + 10 ^ (pH - LYS3))
alb2 = alb2 + 2 / (1 + 10 ^ (pH - LYS4))
alb2 = alb2 + 1 / (1 + 10 ^ (pH - LYS5))
alb2 = alb2 + 50 / (1 + 10 ^ (pH - LYS6))
Rem: 16 different histidine residues
Rem: correction factor to convert HIS pKa from 25 deg C to 37 deg C is approx -0.27
alb2 = alb2 + 1 / (1 + 10 ^ (pH - 7.12 + NB))
alb2 = alb2 + 1 / (1 + 10 ^ (pH - 7.22 + NB))
alb2 = alb2 + 1 / (1 + 10 ^ (pH - 7.1 + NB))
alb2 = alb2 + 1 / (1 + 10 ^ (pH - 7.49 + NB))
alb2 = alb2 + 1 / (1 + 10 ^ (pH - 7.01 + NB))
alb2 = alb2 + 1 / (1 + 10 ^ (pH - 7.31))
alb2 = alb2 + 1 / (1 + 10 ^ (pH - 6.75))
alb2 = alb2 + 1 / (1 + 10 ^ (pH - 6.36))
alb2 = alb2 + 1 / (1 + 10 ^ (pH - 4.85))
alb2 = alb2 + 1 / (1 + 10 ^ (pH - 5.76))
alb2 = alb2 + 1 / (1 + 10 ^ (pH - 6.17))
alb2 = alb2 + 1 / (1 + 10 ^ (pH - 6.73))
alb2 = alb2 + 1 / (1 + 10 ^ (pH - 5.82))
alb2 = alb2 + 1 / (1 + 10 ^ (pH - HIS14))
alb2 = alb2 + 1 / (1 + 10 ^ (pH - HIS15))
alb2 = alb2 + 1 / (1 + 10 ^ (pH - HIS16))
Rem: amino terminus
alb2 = alb2 + 1 / (1 + 10 ^ (pH - 8))
Rem: carboxyl terminus
alb2 = alb2 - 1 / (1 + 10 ^ (-(pH - 3.1)))
alb2 = alb2 * 1000 * 10 * Alb(j) / 66500
Netcharge = Netcharge + alb2
If Abs(Netcharge) < 0.0000001 Then GoTo complete
If Netcharge < 0 Then High = pH
If Netcharge > 0 Then Low = pH
GoTo calculatepH
complete:
Delta = (pH - pHm(j))
sum6 = sum6 + pH
ss = ss + Delta * Delta
s = s + Delta
abvs = abvs + Abs(Delta)
sx = sx + pHm(j)
sxx = sxx + pHm(j) * pHm(j)
sy = sy + pH
syy = syy + pH * pH
sxy = sxy + pHm(j) * pH
Print #2, "DATA"; j; ","; SID(j); ","; PCO2(j); ","; Pi(j); ","; Alb(j); ","; pHm(j); ","; pH; ","; Delta; ","; Delta * Delta
Next j
Close #2
Open "model-results" For Output As #1
n = 65
Print #1, "N = ", n
Print #1,
Print #1, "Checksum1 for pHm =", sum1
Print #1, "Checksum2 for SID =", sum2
Print #1, "Checksum3 for PCO2 =", sum3
Print #1, "Checksum4 for Pi =", sum4
Print #1, "Checksum5 for Alb =", sum5
Print #1, "Checksum6 for pH = ", sum6
Print #1, " "
Print #1, "Sum of Deviations = ", s
Print #1, "Mean Deviation = ", s / n
Print #1,
Print #1, "Sum of Absolute Deviations = ", abvs
Print #1, "Mean Absolute Deviation = ", abvs / n
Print #1,
Print #1, "Sum of Squares of Deviations = ", ss
Print #1, "Root Mean Square Deviation = ", Sqr(ss / n)
Print #1,
SD = Sqr((n * ss - s * s) / (n * (n - 1)))
Print #1, "Standard Deviation = ", SD
Print #1,
Print #1, " "
Print #1, "HIS14 = ", HIS14
Print #1, "HIS15 = ", HIS15
Print #1, "HIS16 = ", HIS16
Print #1, " "
Print #1, "LYS1 = ", LYS1, "n1 = 2"
Print #1, "LYS2 = ", LYS2, "n2 = 2"
Print #1, "LYS3 = ", LYS3, "n3 = 2"
Print #1, "LYS4 = ", LYS4, "n4 = 2"
Print #1, "LYS5 = ", LYS5, "n5 = 1"
Print #1, "LYS6 = ", LYS6, "n6 = 50"
Slope = (n * sxy - sx * sy) / (n * sxx - sx * sx)
incpt = (sy * sxx - sx * sxy) / (n * sxx - sx * sx)
vincpt = sy / n - Slope * sx / n
r = (n * sxy - sx * sy) / Sqr(n * sxx - sx * sx) / Sqr(n * syy - sy * sy)
Var = (syy - incpt * sy - Slope * sxy) / (n - 2)
varslope = n * Var / (n * sxx - sx * sx)
stndevslope = Sqr(varslope)
Rem: t(n-2, alpha/2) for n=65 is 2.3870, where alpha=0.02
t = 2.387
Lconfint = Slope - t * stndevslope
Uconfint = Slope + t * stndevslope
Print #1, " "
Print #1, "slope = ", Slope
Print #1, "intercept = ", incpt
Print #1, "intercept = ", vincpt, "(verify)"
Print #1, "r = ", r
Print #1, "r^2 = ", r * r
Print #1, "Variance = ", Var
Print #1, "Variance of slope = ", varslope
Print #1, "Stnd Deviation of slope = ", stndevslope
Print #1, "98% confidence interval for the slope = ", Lconfint, " to ", Uconfint
Close #1
End Sub
Input Data
01 7.388 49.8 39.3 1.1 7.2
02 7.383 45.4 40 1 7
03 7.521 45.4 26.1 1 7
04 7.389 45.4 38.1 1 7
05 7.217 45.4 62.9 1 7
06 7.315 32.2 23.4 1.2 6.6
07 7.194 32.2 35 1.2 6.6
08 6.979 32.2 68.6 1.2 6.6
09 7.819 71.3 28.9 1.1 6.8
10 7.716 71.3 37.7 1.1 6.8
11 7.504 71.3 65.4 1.1 6.8
12 7.850 70.2 26.4 1 6.8
13 7.719 70.2 37.9 1 6.8
14 7.513 70.2 65.3 1 6.8
15 7.447 45.9 30.8 1 7.1
16 7.375 45.9 38.4 1 7.1
17 7.094 45.9 85 1 7.1
18 7.935 70.2 22.5 1 6.8
19 7.716 70.2 40.2 1 6.8
20 7.423 70.2 83.5 1 6.8
21 7.746 45.8 22.1 1 3.5
22 7.518 45.8 39.9 1 3.5
23 7.218 45.8 85.9 1 3.5
24 7.446 24.2 21.9 0.9 3.4
25 7.226 24.2 39.8 0.9 3.4
26 7.018 24.2 69.7 0.9 3.4
27 7.676 63.7 40.2 1 3.6
28 7.369 63.7 86.7 1 3.6
29 7.711 75.5 38.6 1 6.7
30 7.702 76.4 38.2 1 7.3
31 7.630 65.9 37.9 1 7.3
32 7.572 60.2 35.1 0.7 7.6
33 7.718 58.9 41 1 1.7
34 7.510 58.9 67.9 1 1.7
35 7.399 58.9 88 1 1.7
36 7.684 70.4 38.2 1 7
37 7.477 70.4 65.4 1 7
38 7.390 70.4 85.7 1 7
39 7.551 53.5 38.7 1 6.2
40 7.348 53.5 68.4 1 6.2
41 7.240 53.5 86.3 1 6.2
42 7.598 51.2 41.2 0.9 1.9
43 7.378 51.2 69.8 0.9 1.9
44 7.307 51.2 87.7 0.9 1.9
45 7.320 32.5 22.5 1 8
46 7.144 32.5 38.9 1 8
47 7.006 32.5 59.2 1 8
48 7.416 28.5 22.7 1 2.9
49 7.213 28.5 40.3 1 2.9
50 7.068 28.5 58.6 1 2.9
51 7.460 22.8 23.1 1 1.6
52 7.246 22.8 40.2 1 1.6
53 7.083 22.8 60.6 1 1.6
54 7.125 23.7 22.6 1 5.7
55 6.968 23.7 40 1 5.7
56 6.849 23.7 58 1 5.7
57 7.254 21.4 23 1 3.5
58 7.051 21.4 40.7 1 3.5
59 6.924 21.4 58.3 1 3.5
60 7.654 67.5 39.7 1 7.2
61 7.508 67.5 56.9 1 7.2
62 7.347 67.5 87 1 7.2
63 7.706 62.5 40.1 1 3.8
64 7.561 62.5 57.5 1 3.8
65 7.386 62.5 91.2 1 3.8


